Discrete Mathemetics 试题调研

命题逻辑初步&推理规则&推理系统&谓词逻辑&证明方法

做题记忆知识点

• 命题联结词的优先级自高到低分别为:
• 补充：对偶式和对偶式定理。
• 
• 注意，当是蕴含，仅当是反蕴含，只要就是蕴含，只有才是反蕴含，要么要么请咨询本班TA按照“或”还是“亦或”给分。
• 直接证明法，间接证明法（逆否），（广义）归谬法，分情形证明，构造证明（一般构造和特例），前件假证明法，后件真证明法。

题目

逻辑等值式的证明

1. 列真值表
2. 通过逻辑等价推导
   None.

寻找成真指派，可满足性

1. 不可满足分情况讨论即可
2. 可满足构造一组解即可

用命题逻辑进行推理（不含谓词）

将自然语言转化为谓词

1. 注意标明论域
2. 注意涵盖所有情况，且充要
3. 注意自然语言概念到形式语言的准确转化（如：一元二次方程）

None.

用命题逻辑进行推理（含谓词）

注意：在给出的证明过程中，全称引入和存在引入的逻辑是隐式的，也就是说，在示例的推理中，究竟是存在成立的还是对所有都成立，表述上是没有区别的。
另外，是否可以带着全称量词直接推理（论域相同时），请参考自己班上TA的标准。

• 
• 

证明方法的灵活使用

唯一性证明：同一法。
关于非构造性的存在性证明：尽量构造出一个“自指”的结构。
不失一般性(WLOG)的使用。

集合论&集合代数&关系及其性质&函数&集合的基数

做题记忆知识点

绝对补
亦或（对称差）满足结合律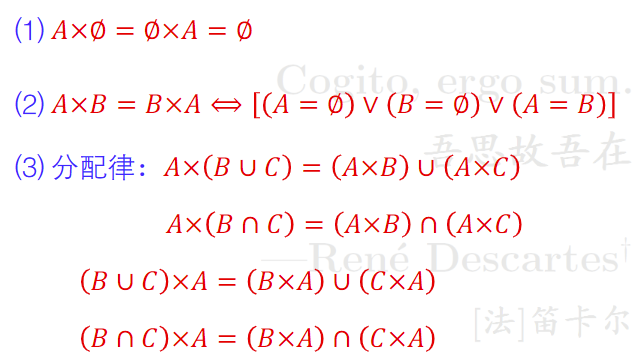

是A→B

证明A成立除非B，需要说 不是B，A成立+是B，A不成立

题目

集合公式的证明

1. 定义
2. 在定义里做逻辑运算
3. 用已知恒等式

   充要的证明，可以推导一圈推导回自身。

注意是不是真子集的问题！！

证明双射函数&单射&满射

函数命题的证明

证明是无穷集

反证法，依据有穷定义，构造一个不在该1-1onto中的。

证明可数集，不可数集，等势

1. 构造1-1onto
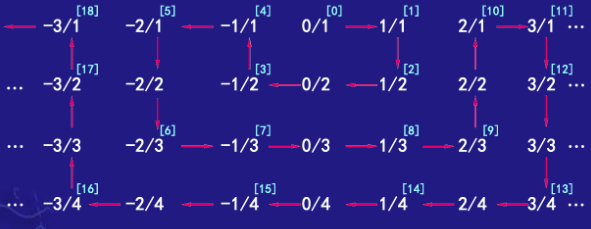
2. Cantor Diag Argu
3. 三明治定理
   一些典型的构造：

• 仿射（证明任意两个实数区间等势）（转化成代数语言）
• 黎曼证明（证明区间和R等势）区间和缺点圆周等势而与R等势（转化成代数语言）
• 有限维度的点均等势
  每个坐标小数点后第i个数一次排列连接
• 幂集的势
  构造子集的特征函数
• 有理数可列
  
• 可列个可列集的并集可列
  斜线排列
• 可数集的并集
  分别放在偶数和奇数上（类似地，放在mod3余0,1,2上）
  可以用的定理
  
  
  

证一个东西不可数，是一个不可数大集合的一部分，只需要证其他的部分是可数的就可以了

容斥原理

数论

题目

整除问题

1. 差分法+归纳
2. 费马小定理和欧拉定理
3. 注意质数大于2全是奇数这件事，2k+1代入看性质
4. 不满足定理使用条件的时候，看可不可以分类讨论
5. 注意只因数分解（小黑子）

同余方程组

1. 中国剩余定理
2. 反向替换法

递归与数学归纳

题目

用第一/第二数学归纳法证明

用结构归纳法证明

排列组合

离散概率