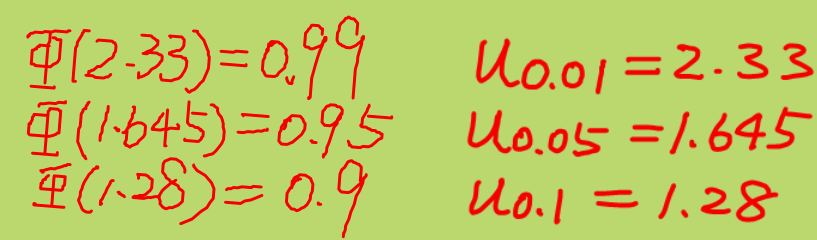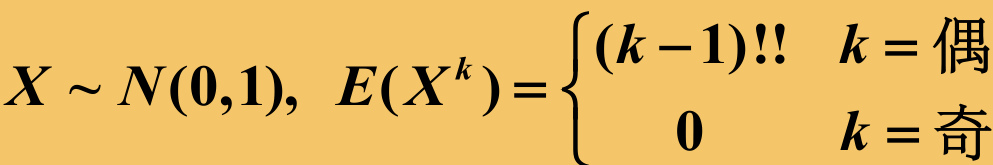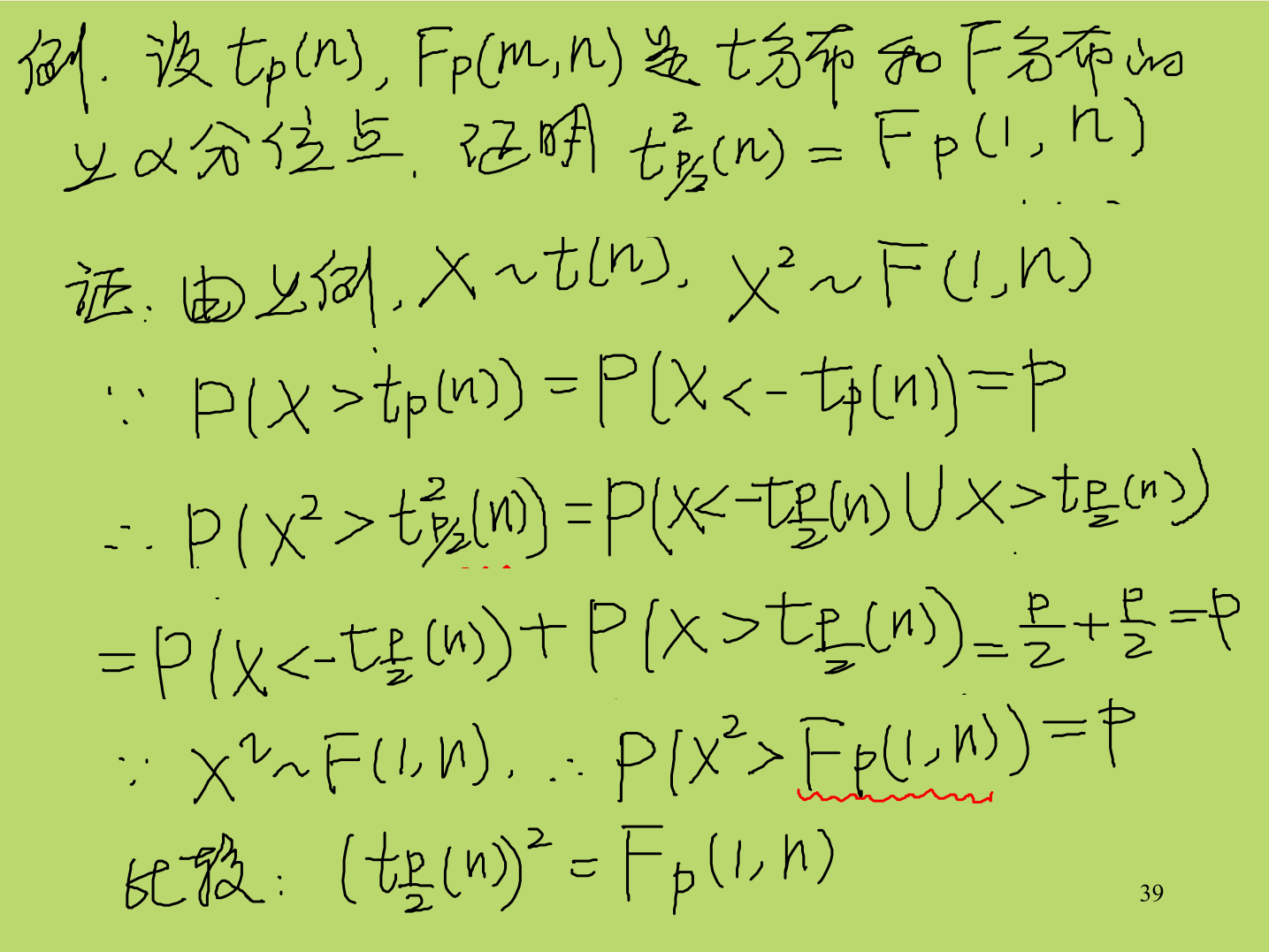概统笔记

Jackcui NJU Loser
  2023-09-04 13:16:19 2023-09-04 13:16 Created   2024-01-02 15:26:52 2024-01-02 15:26 Updated    3.2k Words  11 Mins  

Reference

概统 南大版 傅冬生等著

事件运算

(1)
(2)
(3)
(4)
交换律:
结合律:
分配律:
德摩根(De Morgan)定律:

公理化概率，概型，条件概率

  • 可列可加性：（不相容）
  • 加法定理: （容斥）
  • 抽签原理（抽签概率跟顺序无关）
  • 不放回抽样：
  • 有放回抽样：
  • 球放盒子不重复（）:
  • 全概率公式：
  • 贝叶斯公式：

补充：组合数的计算

概率计算技术

  1. 老老实实利用概型
  2. 条件概率
  3. 缩小样本空间（谨慎！谨慎！谨慎！）

值得注意的题目

1.18，1.21

独立性

  • 若随机事件与相互独立,则与、与、与也相互独立。
  • 设事件相互独立,将其任意分为没有公共事件的个组,每个组任意作事件运算,得到一个新事件,则这个新事件相互独立。
  • 小概率事件原理：随机试验中某事件发生的概率为,无论多么小,只要不断独立重复地做次试验, 迟早会发生的概率为1。
  • n重伯努利实验：泊松定理： 为常数 近似条件（）

值得注意的题目

1.26 ppt 0.001的机床

随机变量及其分布

  • DEFINE 分布函数

离散型随机变量

  • 0-1分布，二项分布…
    服从二项分布的表示
  • 泊松分布（大量试验中稀有事件的出现频数）
    表示：
  • 几何分布（伯努利实验第一次成功的次数）
    表示：
    几何分布无记忆性

    注意泊松分布包括0，几何分布不包括0.

连续型随机变量

  • 均匀分布

    分布函数
    表示：

  • 指数分布
    分布函数
    表示：
    无记忆性：(指数分布可以看作几何分布的连续形式)
    是 取值的平均值。

  • 正态分布
    分布函数
    表示：
    性质：

    • 对称，渐进（显然，否则不收敛）

    • 最值点为，最值为

    • 拐点为

      标准正态分布：
      标准化：

  • 定理： 若 的分布函数 严格单调递增，则随机变量 服从 上的均匀分布

随机变量函数

  • 离散随机变量
    • 一言以蔽之，线性叠加。
  • 连续随机变量
    • 分布函数法：先积分后求导。
    • 服从 分布。
    • 定理： 取值范围为 , 处处可导,且恒有 (或恒有 )

      其中, 为的反函数。

多维随机变量及其函数

  • 联合分布函数

    最下最左极限为0，最上最右极限为1.
  • 对任意实数,有 （矩形区域非负）

  • DEFINE 独立

    或
  • 随机变量独立性的一个重要性质:相互独立, , 为的连续或分段连续函数,则随机变量的函数与相互独立。

二维离散随机变量

边缘分布
记为
同理。
独立条件即为
常用分布

  • 三项分布（三种有放回）
  • 二维超几何分布（三种无放回）
的函数

求和即可
*泊松分布，二项分布具有可加性

二维连续随机变量

边缘分布


独立条件即为
或 $\int_{-\infty}^x \int_{-\infty}^y p(u, v) \mathrm{d} u \mathrm{d} v =\int_{-\infty}^x \int_{-\infty}^y p_X(x) p_Y(y) \mathrm{d} x \mathrm{d} y$
关注：例3.8

常用分布

  • 二维均匀分布（就是几何概型）
  • 二维正态分布 Missing or unrecognized delimiter for \leftp(x, y)= \frac{1}{2\pi \sigma_1\sigma_2\sqrt{1-\rho^2}} \exp \left{-\frac{1}{2\left(1-\rho^2\right)}\left[\left(\frac{x-\mu_1}{\sigma_1}\right)^2\right.\right. \left.\left.-2\rho\left(\frac{x-\mu_1}{\sigma_1}\right)\left(\frac{y-\mu_2}{\sigma_2}\right)+\left(\frac{y-\mu_2}{\sigma_2}\right)^2\right]\right}
  • 定理
    • 的边缘分布为 。
    • 相互独立的充要条件为 。
的函数
  • 连续的离散（离散）
    一次求即可
  • 连续的连续（连续）
    依然使用分布函数法
    3.18 题
    • 常用 函数分布公式
    • 和的分布


      相互独立的情况（卷积公式）


      特别地，
    • 差的分布

      3.20 题
    • 积的分布
    • 商的分布
    • 相互独立情形下的 分布

  • 有连续有离散： 把离散的当成划分样本空间，用全概率公式。
    3.23

随机变量的数字特征

数学期望

离散型

要求级数 绝对收敛

常用分布的数学期望

  • 二项分布
  • 泊松分布
  • 几何分布 （处理注意级数求和技术）

的函数的

高维：

连续型

要求积分 绝对收敛

不一定存在：
连续型Cauchy分布：
尽管是关于轴对称，但就是不存在。

常用分布的数学期望

  • 均匀分布
  • 指数分布
  • 正态分布

的函数的

定理：


注意：用不用上述的定理要辩证的看待，因为有时候求密度函数反而比较简便。

性质

线性性质：
若相互独立：
用性质来简化运算：计算二项和超几何分布的期望。

方差

方差
标准差

常用
  • 二项分布
  • 泊松分布
  • 均匀分布
  • 指数分布
  • 正态分布
性质
  • 如果独立

切比雪夫不等式


注意：方差为0→几乎处处为常数（未细究）

协方差



性质
  • 对称：
  • 提常数：
  • 线性：
  • 若独立：
Cauchy-Schwarz不等式


取等条件：存在常数 使得

相关系数

标准化随机变量 ()

$\rho_{X Y}(或Corr(X,Y))=Cov(X^*,Y^*)=E\left(X^{} Y^{}\right)=\frac{Cov(X, Y)}{\sqrt{D(X)} \sqrt{D(Y)}}相关系数是随机变量标准化后的协方差。（把协方差压缩到[-1,1]空间内）线性无关：\rho_{X Y}=0等价条件cov(X, Y)=0E(X Y)=E(X) E(Y)D(X\pm Y)=D(X)\pm D(Y)$
定理：若 独立,则线性无关。反之则不一定成立。

对于正态分布，独立和线性无关是等价的。

矩

矩的概念统摄了数学期望、方差等数字特征。

  • 阶原点矩
  • 阶中心矩

方差即为二阶中心矩。

正态分布的中心矩：

  • 偶数：
  • 奇数：

三阶中心矩：偏度
四阶中心矩：峰度

协方差矩阵

定义



（对称阵）
二维正态分布的协方差矩阵：
由此得二维正态分布密度函数协方差阵表示形式：

值得关注的题

到教材92页；

大数定律

抽样分布

统计量：
（注意这是个函数，所以是大写的随机变量）
样本具体的值：
（注意这个是样本具体的值，所以是小写）

  • 样本均值：
  • 样本方差：
  • 修正的样本方差：
  • 样本标准差：
  • 样本阶(原点)矩:
  • 样本 阶中心矩: $\boldsymbol{B}{\boldsymbol{k}}=\frac{1}{\boldsymbol{n}} \sum{i=1}^n\left(X_i-\bar{X}\right)^{\boldsymbol{k}} \quad \boldsymbol{k}=\mathbf{1}, \boldsymbol{2}, \cdots$

    注意：总体k阶矩： 不是统计量

重要结论：

  • 则
    特别地，若 则
  • 样本方差为：

样本的函数分布

  • 线性函数：从略。

    上分位点：{}
    图片.png

    图片.png

  • 注意从此开始的三种分布，结构和分布是充要的，有结构则服从分布，有分布则存在对应结构。
  • 分布
    相互独立,

    • 概率密度从略

    • 图片.png

    • 性质：
      可加性：
      统计特征：

      推导中用到的性质：图片.png

    • 计算：

      • 查表。
      • 估计公式：对于, 是N(0,1)上分位点。
  • 分布
    , 独立

    则 .
    • 性质：
      n比较大时趋于正态分布：
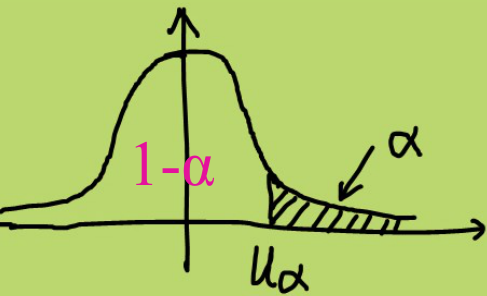
      对称性：
    • 求值：
      • 查上分位点表。
      • 近似：时,对于常用的值,可用正态近似:
  • 分布
    ，独立

    .
    • 性质：
      ,则.
    • 求值：
      • 查表。
  • 一些结论和方法：
    • 则
    • 还原到分位点的事件区间去讨论
      图片.png

最为重要结论：样本均值和方差的分布

前提： 来自正态总体


  • 或
  • 和 相互独立

  • 或

    啊？

注意区分：

,与独立.
和 分别是 的修正样本方差.

  • .
  • .
  • ,

    其中.

小蓝书：

  • 那种构造题，核心是构造统计量（消掉参数）。
  • 求往往就是求D(X)（因为是无偏估计）。

参数估计

矩估计

无论总体X服从何种分布,总体均值 ，总体方差作为未知参数,其矩估计量一定是样本均值和样本方差,即:

??? 究竟什么是样本方差，这里为什么又变成了 ???

注意： 对于一般的分布， 的矩估计量是 （但是有偏）, 无偏估计量是 （或者记为 ），但 不是 的无偏估计量； 对于正态分布的总体，其方差的极大似然估计是 。因而 的极大似然估计就是 （而不是 ）。

相关系数的矩估计：

可能会出现某一阶矩不能用来估计的情况。

极大似然估计

使似然函数取极大值。
原函数、对数。
技巧见作业。
特别地，

离散随机变量：设湖中有鱼N条,现捕出r条,做上记号后放回湖。一段时间后再捕出条,结果其中有条标有记号。试根据此信息,估计湖中鱼的数目N。

极大似然估计的不变性

极大似然估计点可以套函数（函数必须是具有单值反函数）

估计量的评价

  • 无偏性：
  • 有效性：
  • 一致性：
    关于一致性的结论
    • 样本K阶矩是总体K阶矩的一致估计量
    • 如果是无偏估计量且n趋于无穷时方差趋于0，则是一致估计量
    • 矩法得到的估计量一般是一致估计量

区间估计

区间估计是求出一个由统计量确定的区间，使得该区间包括被估计的真值的概率大于等于可靠度。

  • 置信区间的长度反映了估计精度， L越小,估计精度越高.
  • 反映了估计的可靠度, 越小,1- 越大,估计的可靠度越高
    但这时, 往往增大,因而估计精度降低.
  • 确定后,置信区间的选取方法不唯一,常选长度最小的一个.
正态总体的区间估计
  • 单正态总体的 均值估计
    • 已知方差

      显然可以找出无数个区间满足，一般取对称区间（因为最短）
    • 未知方差

      还是取对称区间
  • 单正态总体的 方差估计

    分布不再对称，但可以取使两侧区间外概率对称的点。
  • 双正态总体 均值之差估计 已知 （未知的呢？？？）

    显然区间为
  • 双正态总体 方差之比估计

区间为

  • 单侧区间，方法比较类似，题没细看。
非正态总体的区间估计

大样本法：
图片.png

小蓝书：

  • 记一个积分：零点正态分布加绝对值的期望：
  • 积分
  • 注意只求期望的时候不一定非要求出分布，多尝试利用D,E关系往里转移。

    12.3 12.10？？？

  • 无偏性有效性说白了就是算期望算方差，这里一定要注意方法多样性，是利用数字特征的性质，还是用定义来积分。
  • 评注：
    • 矩估计不一定存在（柯西），可能不唯一（泊松）。
    • 无偏估计量不一定存在（两点）
    • 一致估计量可能不唯一
    • 最大似然估计量可能不唯一
    • 似然方程的解不一定是最大似然估计量
    • 无偏估计可能不合理（可能正负都不对）
  • 超多参数处理技巧
    图片.png

假设检验

原理是小概率事件原理。

一般取5%

概率意义下的反证法。
假设检验五要素：
图片.png
实例：
图片.png
图片.png

如果一个统计假设完全确定总体的分布,则称为简单假设,如,否则称为复合假设,如,或 。

在正态的前提下，界限即是

两类错误：
弃真错误：本来对的当成错的
存伪错误：本来错的当成对的

弃真错误： 拒绝 为真 为真
( 有时候也被称为显著性水平)
存伪错误： 接受 为假 为假

给定样本容量的情况下,犯两类错误的概率不可能同时减小,减少其中一个,另外一个会增大。

求 的例子：
图片.png
图片.png

正态总体的假设检验具体情形

注意其实就是各种检验，区别主要产生于对总体的已知情况，如果已知总体的参数较少，就要用更多的统计量来代替，从而就会产生区别。

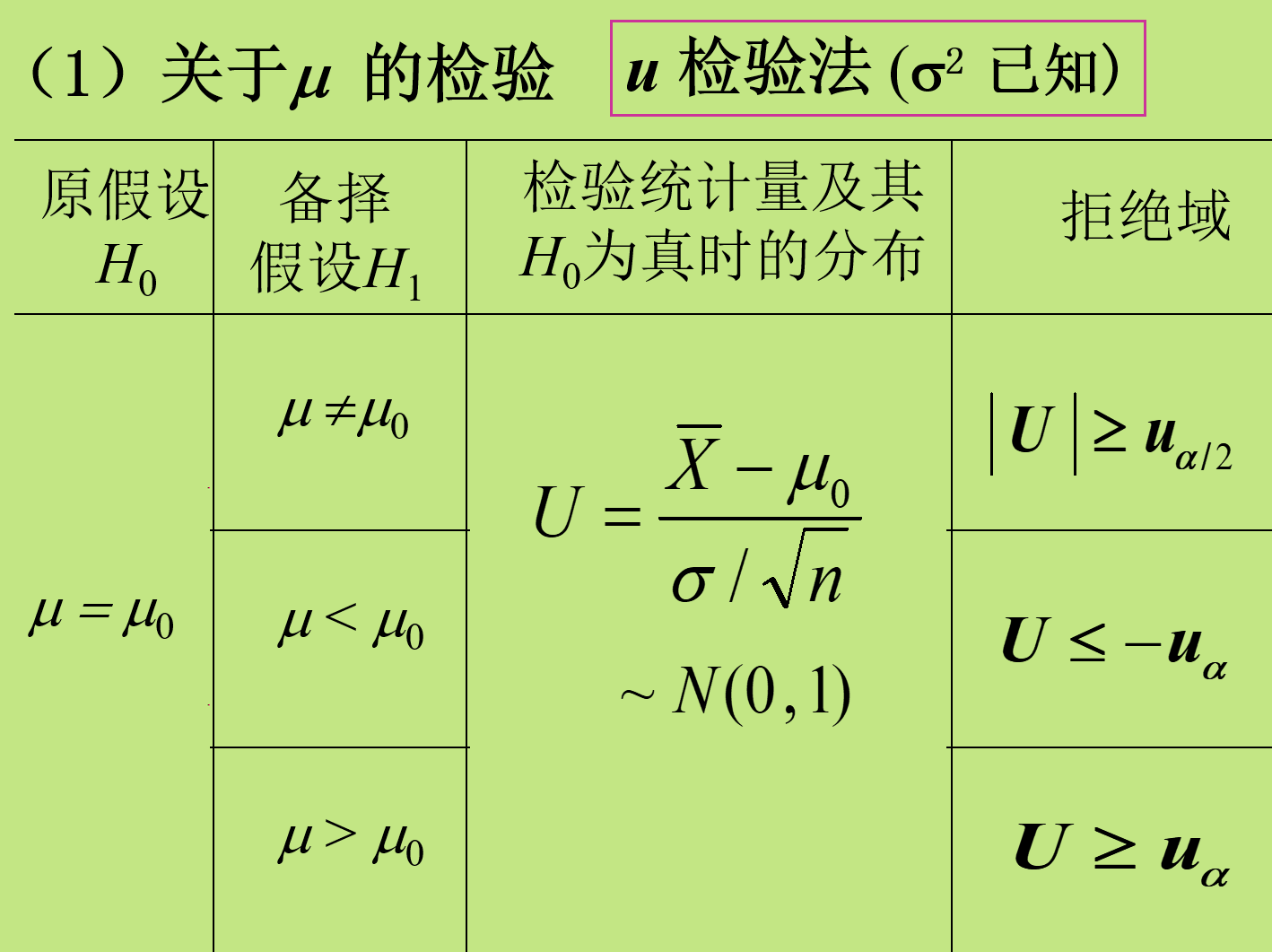
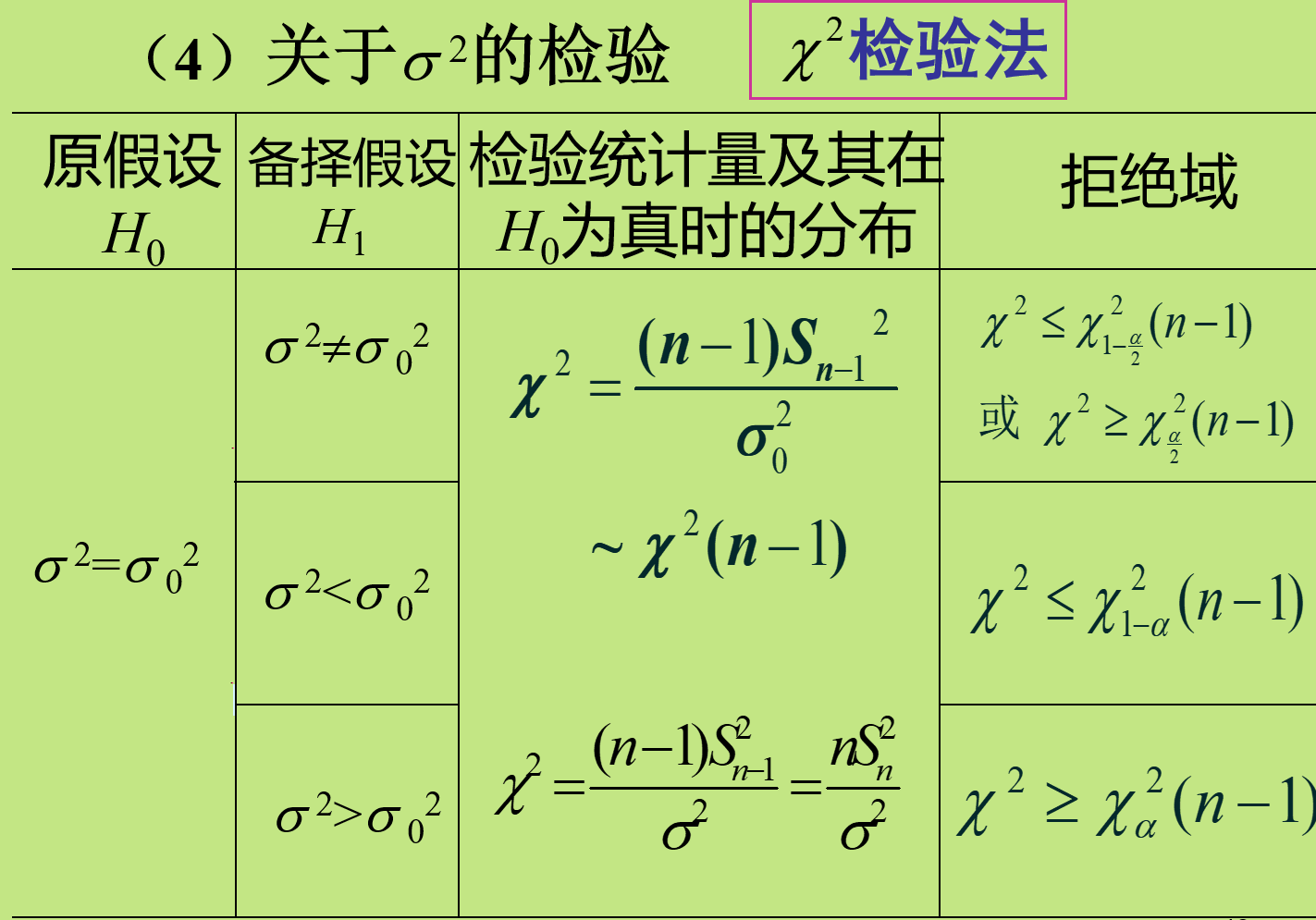
  • 检验

    • 已知
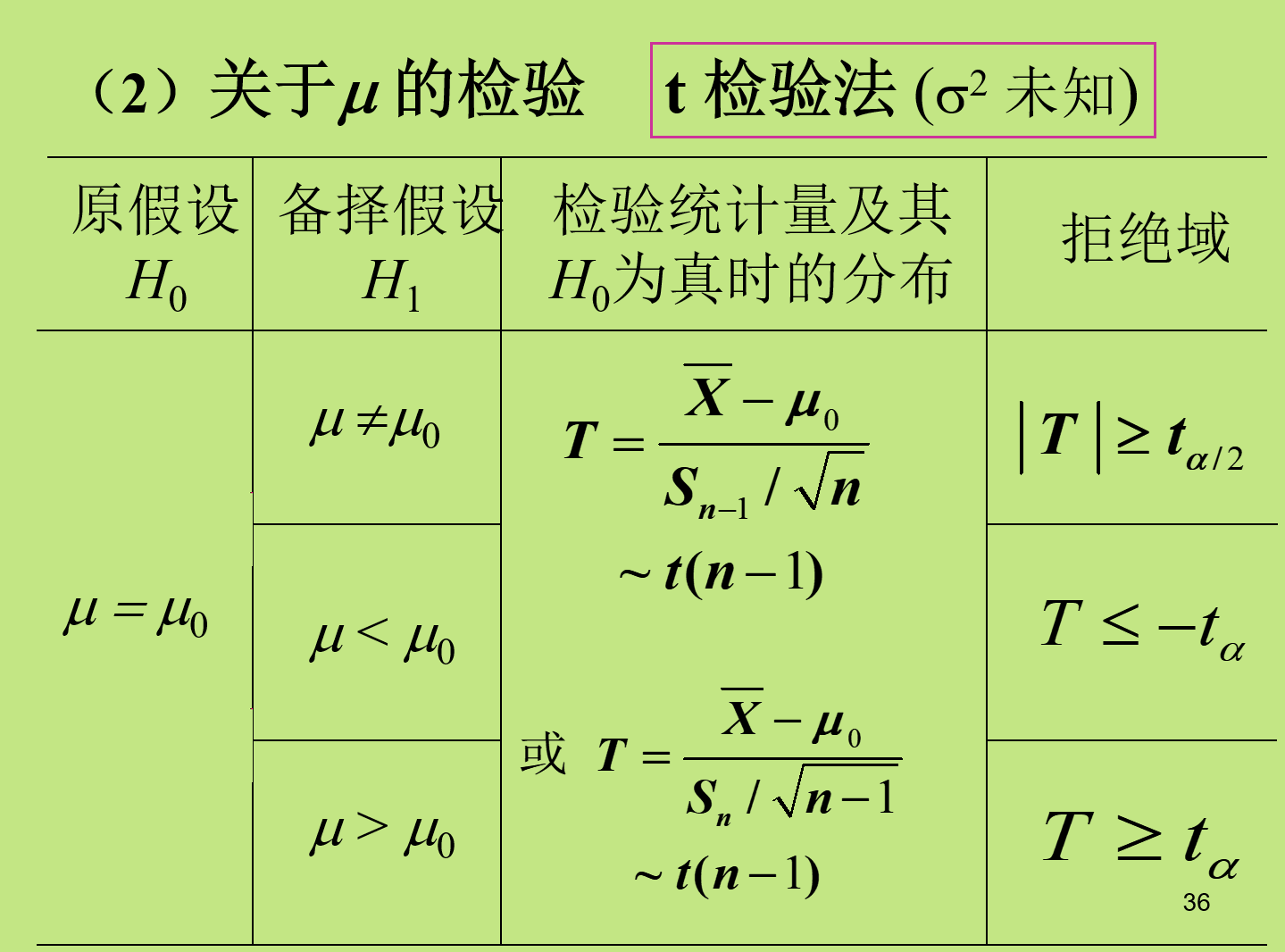
      图片.png
    • 未知
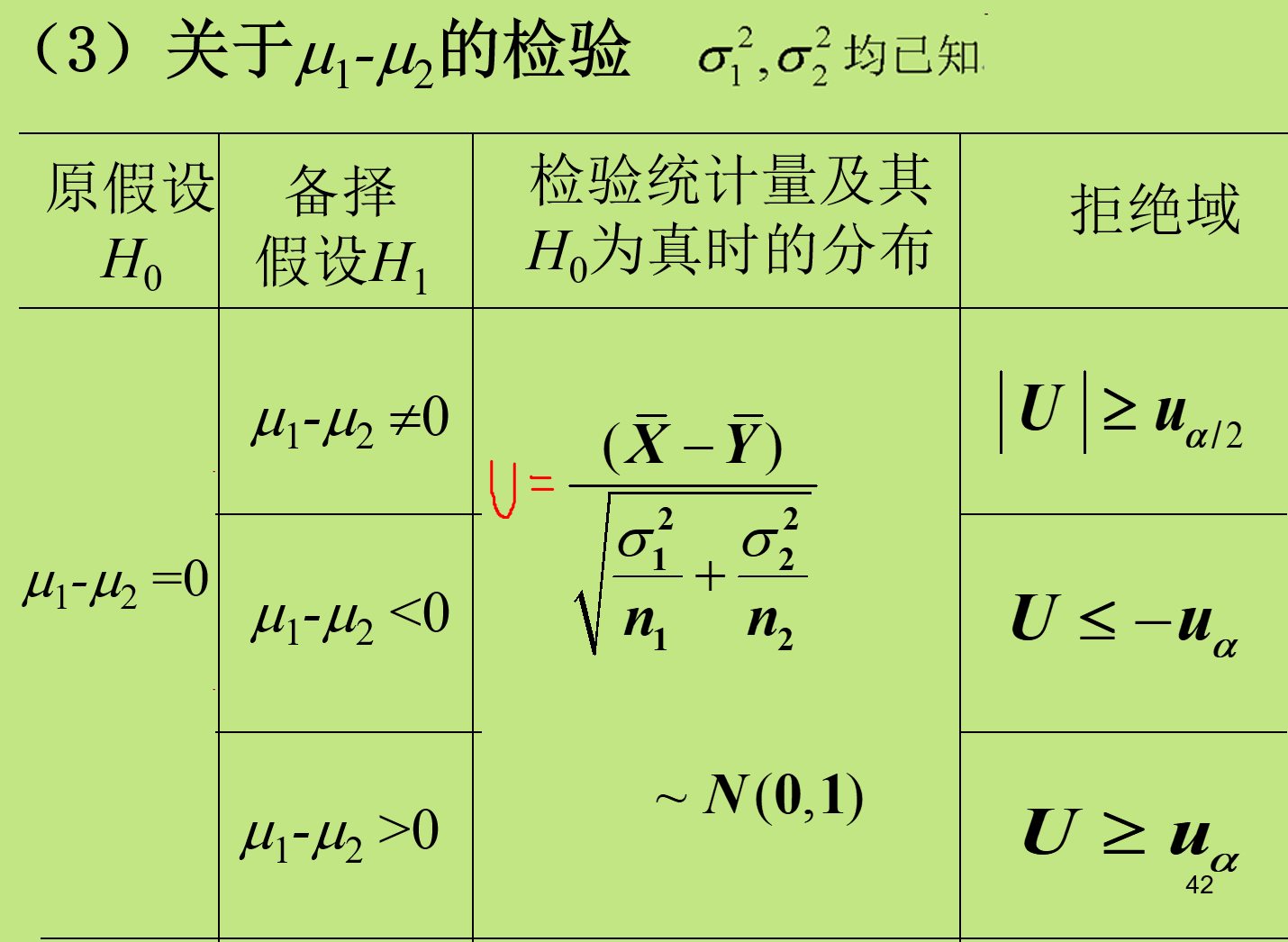
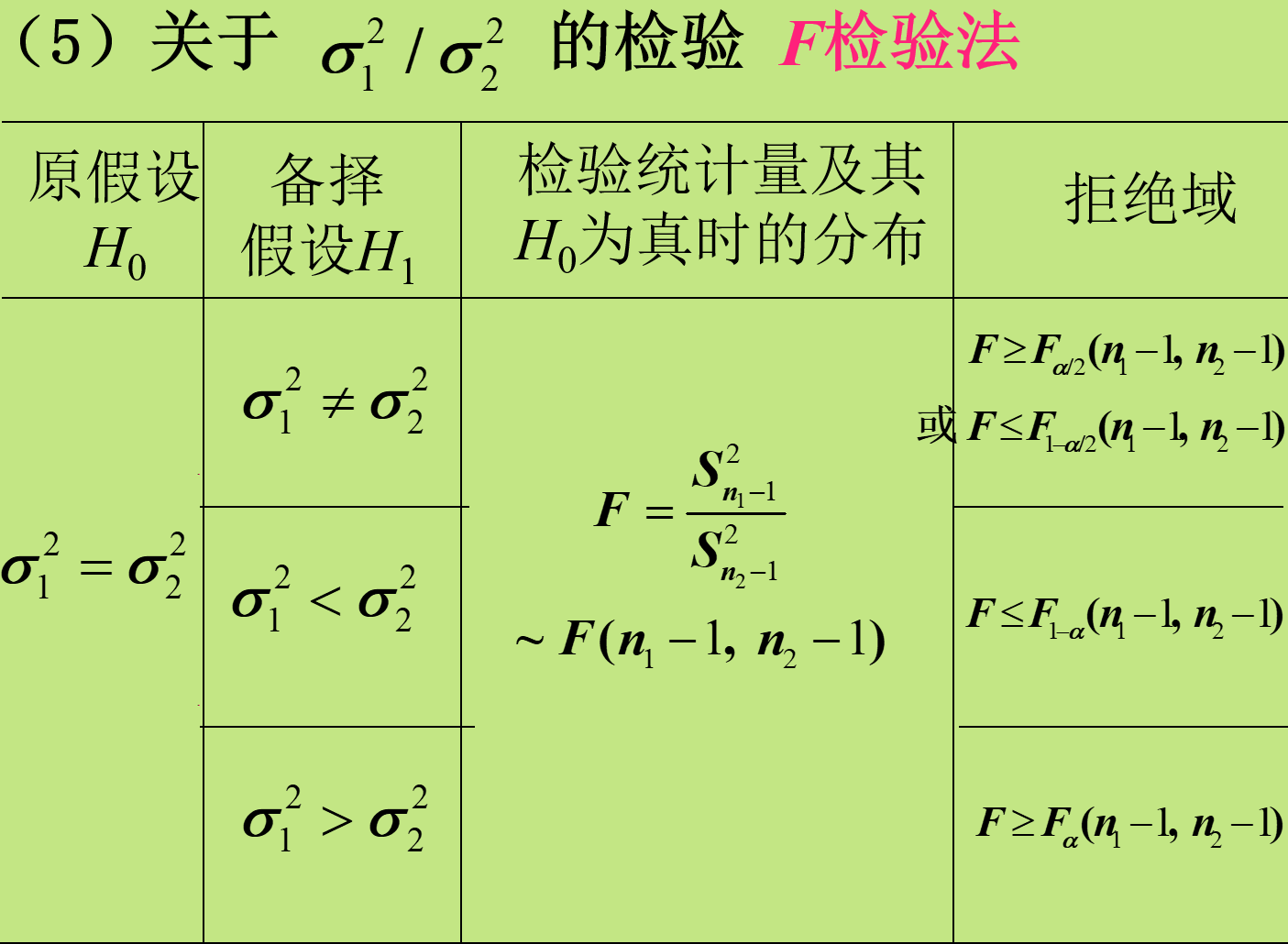
      图片.png

  • 检验 之差
    设来自, 来自，相互独立。， 样本均值, ，样本方差（ 注意是修正的。。。 ）

    • 均已知
      图片.png
    • 未知但相等


      {}

  • 检验
    图片.png

  • 检验
    图片.png

非正态总体的假设检验

足够大，关于均值的，就按照上面的算就可以。

由中心极限定理？ 待复习

关于分布函数的假设的检验：拟合优度检验

从略。

  • Post title：概统笔记
  • Post author：Jackcui
  • Create time：2023-09-04 13:16:19
  • Post link：https://jackcuii.github.io/2023/09/04/prosta/
  • Copyright Notice：All articles in this blog are licensed under BY-NC-SA unless stating additionally.
 Comments
On this page
概统笔记
  1. Reference
  2. 事件运算
  3. 公理化概率，概型，条件概率
    1. 补充：组合数的计算
    2. 概率计算技术
    3. 值得注意的题目
  4. 独立性
    1. 值得注意的题目
  5. 随机变量及其分布
    1. 离散型随机变量
    2. 连续型随机变量
  6. 随机变量函数
  7. 多维随机变量及其函数
    1. 二维离散随机变量
      1. 的函数
    2. 二维连续随机变量
      1. 的函数
  8. 随机变量的数字特征
    1. 数学期望
      1. 离散型
      2. 连续型
      3. 性质
    2. 方差
      1. 常用
      2. 性质
    3. 切比雪夫不等式
    4. 协方差
      1. 性质
      2. Cauchy-Schwarz不等式
    5. 相关系数
    6. 矩
    7. 协方差矩阵
      1. 定义
    8. 值得关注的题
  9. 大数定律
  10. 抽样分布
    1. 样本的函数分布
    2. 最为重要结论：样本均值和方差的分布
  11. 参数估计
    1. 矩估计
    2. 极大似然估计
      1. 极大似然估计的不变性
    3. 估计量的评价
    4. 区间估计
      1. 正态总体的区间估计
      2. 非正态总体的区间估计
  12. 假设检验
    1. 正态总体的假设检验具体情形
    2. 非正态总体的假设检验
    3. 关于分布函数的假设的检验：拟合优度检验