Data Structure Notes

Jackcui NJU Loser
  2023-09-07 18:51:13 2023-09-07 18:51 Created   2023-11-02 11:55:39 2023-11-02 11:55 Updated    1.5k Words  6 Mins  

Preface

面向课内考试的归纳功利化整理。

*关于数据结构的形而上

参见ch1.pdf,P1-P34.

数据结构种类

线性结构，层次结构，群结构。（记住这仨词儿）

算法复杂度分析

程序步

注释：程序步数为0
声明语句：程序步数为0
表达式、赋值语句：程序步数为1
循环语句：循环控制语句每次执行的程序步数为1

注意：increment, decrement, self-assignment 全算一步。

你说的有道理，但答案是这么写的（该扣分还是要扣）。
———— 助教

…

渐进复杂度分析

$O(f(n))$而已，即决定数量级。
Ontario.

String

String の Class 实现（基础部分）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
#ifndef ASTRING_H	//定义在文件“Astring.h”中
#define ASTRING_H
#define defaultSize = 128;     //字符串的最大长度
class AString {
//对象: 零个或多个字符组成的一个有限序列。
private:
    char *ch;			      //串存放数组
    int curLength;		      //串的实际长度
	int maxSize;		      //存放数组的最大长度
public:    
    AString(int sz = defaultSize);      //构造函数 	
    AString(const char *init );          //构造函数
    AString(const AString& ob);      //复制构造函数
    ～AString() {delete [ ]ch; }	      //析构函数
    int Length() const { return curLength; }	 //求长度
    Astring& operator() (int pos, int len);   //求子串
    bool operator == (AString& ob) const 
        { return strcmp (ch, ob.ch) == 0; }
	    //判串相等. 若串相等, 则函数返回true
    bool operator != (AString& ob) const 
        { return strcmp (ch, ob.ch) != 0; }
	   //判串不等. 若串不相等, 则函数返回true  
    bool operator ! () const { return curLength == 0; } 
	   //判串空否。若串空, 则函数返回true
    AString& operator = (AString& ob);      //串赋值
    AString& operator += (AString& ob);	//串连接
    char& operator [ ] (int i);		//取第 i 个字符
    int Find (AString& pat, int start) const;    //串匹配
};
AString::AString(int sz) {
//构造函数：创建一个空串
     maxSize = sz;
     ch = new char[maxSize+1];        //创建串数组
     if (ch == NULL) 
         { cerr << “存储分配错!\n”;  exit(1); }
     curLength = 0;       
     ch[0] = ‘\0’;
};
AString::AString(const char *init) {
//复制构造函数: 从已有字符数组*init复制
     int len = strlen(init);
     maxSize = (len > defaultSize) ? len : defaultSize;
     ch = new char[maxSize+1];     //创建串数组
     if (ch == NULL)
        { cerr << “存储分配错 ! \n”;  exit(1); }
     curLength = len;	 	   //复制串长度
     strcpy(ch, init);		             //复制串值	
 }；
AString :: AString(const AString& ob) {
 //复制构造函数：从已有串ob复制
     maxSize = ob.maxSize;               //复制串最大长度
     ch = new char[maxSize +1];     //创建串数组
     if (ch == NULL) 
         { cerr << “存储分配错! \n”;  exit(1); }
     curLength = ob.curLength;          //复制串长度
     strcpy(ch, ob.ch);                         //复制串值
 };	
AString  AString::operator () (int pos, int len) {
//从串中第 pos 个位置起连续提取 len 个字符形成
//子串返回 	
     AString  temp;                           //建立空串对象
     if (pos >= 0 && pos+len-1 < maxSize && len > 0)
     {                                                  //提取子串
	      if (pos+len-1 >= curLength)  
               len = curLength - pos;     //调整提取字符数
          temp.curLength = len;           //子串长度
          for (int i = 0, j = pos; i < len; i++, j++) 
	           temp.ch[i] = ch[j];        //传送串数组
	      temp.ch[len] = ‘\0’;           //子串结束
     }
     return  temp;
};	
AString& AString::operator = (const AString& ob) {
     if (&ob != this) {	//若两个串相等为自我赋值
          	delete []ch; 
		ch = new char[maxSize+1];	//重新分配 
	     	if (ch == NULL) 
              { cerr << “存储分配失败!\n ”;  exit(1); }
		curLength = ob.curLength;  strcpy(ch,ob.ch);
     }
	 else cout << “字符串自身赋值出错!\n”;	
	 return this;
}; 
char AString::operator [ ] (int i) {
//串重载操作：取当前串*this的第i个字符
     if (i < 0 || i >= curLength) 
         { cout << “字符串下标超界!\n ”; exit(1); } 
	 return ch[i];
};
AString& AString::operator += (const AString& ob)
{
     char *temp = ch;		//暂存原串数组
	 int n = curLength + ob.curLength;	      //串长度累加
	 int m = (maxSize >= n) ? maxSize : n; //新空间大小
	 ch = new char[m];
     if (ch == NULL) 
         { cerr << “存储分配错!\n ”;  exit(1); }
	 maxSize = m;  curLength = n;
	 strcpy(ch, temp);        	         //拷贝原串数组
	 strcat(ch, ob.ch);	         //连接ob串数组  	
     delete []temp;  
     return this;
};

字符串匹配のKMP算法

OI wiki教程(包括一些基于KMP基本思想的拓展思考)
涉及问题索引：
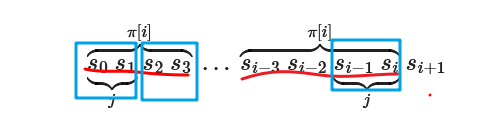
- 前缀函数求解
- KMP算法
- 字符串周期
- 前缀出现次数统计
- 本质不同子串统计
- 字符串分割成周期

前缀函数状态转移
图片.png
KMP
图片.png
比较接地气的详细讲解

广义表

完全不知道制造出这个ADT有什么可说的。。。
头是头，尾是表里其他元素组成的表。
Node 三种类型： 表头，原子，子表
就是Scheme里的List (Python 里其实也是这玩意)

深度定义：其实就是最深的套几层括号。

实现的时候要引用计数，不然多引用的时候，删子表会炸。

Tree

Binary Tree

  • 若二叉树结点的层次从 1 开始, 则在二叉树的第 i 层最多有 2i-1 个结点。
  • 深度为 k 的二叉树最少有 k 个结点，最多有 2k-1个结点。
  • 对任何一棵二叉树，如果其叶结点有 $n_0$ 个, 度为 2 的非叶结点有 $n_2$ 个, 则有$n0＝n2＋1$
  • 具有 n (n≥0) 个结点的完全二叉树的深度为 $log2(n+1)$

线性映射
若$i = 1$, 则 i 无双亲
若$i > 1$, 则 i 的双亲为$[i／2]$
若$2i <= n$, 则 i 的左子女为 $2 i$
若$2i+1 <= n$, 则 i 的右子女为$2i+1$
若 i 为奇数, 且$i != 1$, 则其左兄弟为$i-1$
若 i 为偶数, 且$i != n$, 则其右兄弟为$i+1$

四种遍历
前序中序确定树

三序线索化二叉树

这*东西有什么用？见ppt?

一般树存储

留了一个不知道有什么用的子女兄弟存储（见ppt），剩下的都是废话。

遍历

深搜，广搜，废话连篇，略。

Forest

遍历关注一下广度，就是子女兄弟法。

Heap

二叉堆

以及对顶堆。
https://oi-wiki.org/ds/binary-heap/

Huffman tree

没啥意思，构造就是取小merge。

Reference

NJU DS lwj

  • Post title：Data Structure Notes
  • Post author：Jackcui
  • Create time：2023-09-07 18:51:13
  • Post link：https://jackcuii.github.io/2023/09/07/DS/
  • Copyright Notice：All articles in this blog are licensed under BY-NC-SA unless stating additionally.
 Comments
On this page
Data Structure Notes
  1. Preface
  2. *关于数据结构的形而上
  3. 数据结构种类
  4. 算法复杂度分析
    1. 程序步
    2. 渐进复杂度分析
  5. String
    1. 字符串匹配のKMP算法
  • OI wiki教程(包括一些基于KMP基本思想的拓展思考) 涉及问题索引：- 前缀函数求解- KMP算法- 字符串周期- 前缀出现次数统计- 本质不同子串统计- 字符串分割成周期
    1. 广义表
    2. Tree
      1. Binary Tree
        1. 三序线索化二叉树
        2. 一般树存储
        3. 遍历
      2. Forest
      3. Heap
        1. 二叉堆
      4. Huffman tree
    3. Reference